Domain Basics
In this file, we will explain the usage of the domain classes. Every domain is a child of the main class Domain and implements the following methods and properties:
__contains__: to check if a point lays inside this domainvolume,set_volume: to compute or set the volume of the domainbounding_box: to get a bounding box of the given domainboundary: returns the boundary of the domain, this object itself is a domain and implements the same methods. The boundary also knows the normal vectors. But a boundary itself has no boundary!
For explicit documentation of each method and all implemented domains, see the docs.
All domains can be found under torchphysics.domains.
Some pre implemented domains are: Point, Interval, Parallelogram, Circle...
Here we focus now on the creation of different domains. To create a domain, we need a space to which the domain belongs. The definition of spaces were part of the previous tutorial.
You can find The following code as a notebook here, if you want to try out something yourself. To create the interval [0, 5]:
import torchphysics as tp
T = tp.spaces.R1('t') # we need a one dimensional space
I = tp.domains.Interval(T, 0, 5)
To create the unit square or circle:
X = tp.spaces.R2('x') # we need a two dimensional space
R = tp.domains.Parallelogram(X, [0, 0], [1, 0], [0, 1])
C = tp.domains.Circle(X, [0, 0], 1)
If we want to get the boundary, we use .boundary:
R_bound = R.boundary
C_bound = C.boundary
Now it would be nice to look at the domains directly. For this we have to use the PointSamplers which are part of the next tutorial. There we will explain how to create the following plots.
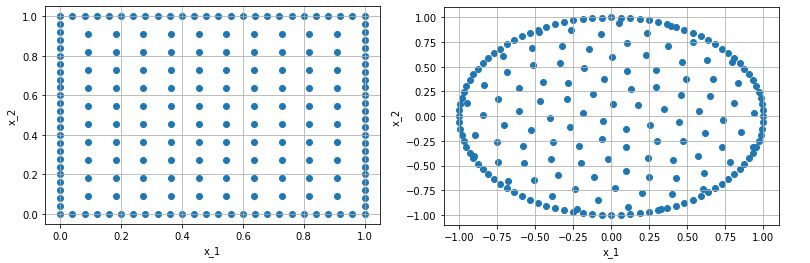
The definition of other basic domains follow the same way.
Domain Operations
Until now we only created simple geometries. For complex domains the following operations are implemented:
Union\(A \cup B\), implemented with:'+'Intersection\(A \cap B\), implemented with:'&'Cut\(A \setminus B\), implemented with:'-'Cartesian product\(A \times B\), implemented with: \(\cdot\)
The only important aspect is that for union, intersection and cut the domains have to belong to the same space. The returning object is a child of Domains and implements all previously mentioned methods. The operation can be used for an arbitrary number of times, but for complex domains, the creation of training points will possibly become costly and slow.
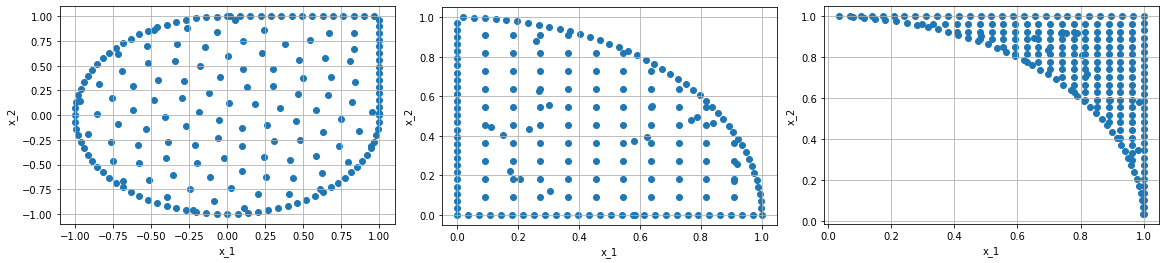
union_domain = R + C
intersection_domain = R & C
cut_domain = R - C
The boundary can be again called with .boundary. Since the operation can create
complex domains the voluem can not always be computed. If a exact value is needed,
one has to set it over the set_volume methode.
Again we can have a look at the corresponding geometries:
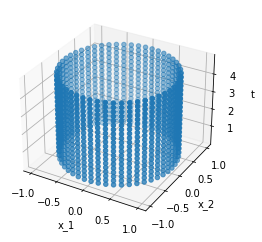
For the product, we create the Cartesian product of an interval and circle to get a cylinder:
cylinder = C * I
The product domain will lay in the product of the spaces. For example, the above cylinder lays now in the space \(X \cdot T\). Here we only show the outer surface:
Changing Domains
The last aspect, is the possibility of variable domains. E.g. a domain that grows in time or a rotating circle. To this end, all parameters that define a domain can also be functions. For example, the radius of the circle or the origin of a parallelogram.
Right now, a domain can only depend on the variables of another domain. So a domain that should change with the trained solution is not possible, for now.
The creation of the domains stays the same, one has to only replace the desired parameters.
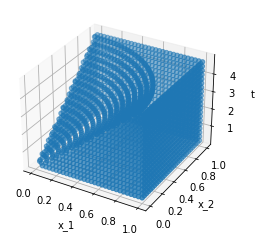
C = tp.domains.Circle(X, [0, 0], lambda t: t/5)
These domains can be used like all the other domains to create a product domain or apply an operation.
new_domain = R - C
If we now plot the product with the interval \(I\), we get:
These are all basic about the creation of different domains, next up is either the creation of polygons and the loading of external objects, or the creation of training/validation points